Di Luca Rizzo.

La generazione di numeri casuali è un campo di ricerca di cruciale importanza nel mondo di oggi. Dalle transazioni bancarie fino ai messaggi che mandiamo ai nostri amici sulle applicazioni di messaggistica privata. Per far si che tutti questi dati siano segreti abbiamo bisogno di numeri casuali. Ad oggi però usiamo dei generatori particolari, perchè in realtà sono altamente prevedibili. Siamo fortunati: i computer di oggi non sono veloci abbastanza per riuscire a prevedere i numeri estratti da questi generatori. La sfortuna: i computer quantistici sono in grado di rivelare i nostri segreti a tutti. Abbiamo ancora tempo però prima che i computer quantistici siano utilizzabili, nel frattempo dobbiamo correre ai ripari.

La soluzione è semplice: generare numeri che siano veramente casuali quindi non deterministici. Vengono in nostro soccorso Randy Kuang e Dafu Lou che nel loro articolo: “IID-Based QPP-RNG: A Random Number Generator Utilizing Random Permutation Sorting Driven by System Jitter” ci forniscono una soluzione al problema completamente software. Esploriamo i concetti necessari a capire il funzionamento di questo nuovo generatore.

Dobbiamo parlare di fisica. Il primo concetto è l’entropia: misura la casualità o informazione di un sistema; proveremo a massimizzare l’entropia nel nostro sistema per avere numeri più casuali possibili. La fisica quantistica, un campo di ricerca intensiva, ha un funzionamento probabilistico e quindi imprevedibile, per questo ci permetterà di massimizzare l’entropia.

QPP (Quantum Permutation Pad) è la prima parte dell’algoritmo. Ci fornisce due valori importanti, capiremo dopo il perchè. Consideriamo una lista di numeri [1, 2, 3, 4, 5], mescoliamola [3, 1, 5, 2, 4]. Proviamo adesso a riordinare la lista finché non è in ordine crescente ([1, 2, 3, 4, 5]). Da questo processo otteniamo: il tempo necessario a riordinare la lista, i tentativi necessari per riordinare la lista. Questi dati sono governati da processi quantistici, decisioni del sistema operativo, fluttuazioni energetiche, componenti della macchina e da casualità combinatoria (\( 1\over{n!} \)): quindi possiamo dire, grazie a questa operazione , di aver accumulato molta casualità. Sono dati un po’ grezzi e non vanno bene in questa forma quindi dobbiamo raffinarli. Passiamo questi dati nelle equazioni: \(N \text{(numero tentativi)} \mod 256 \) e \(\text{SystemJitter (tempo di esecuzione)} \mod 256 \) che ci fornirà un valore tra [0, 255] oppure otto bit di informazione. L’operazione di modulo significa prendere il resto di una divisione, per esempio: \(15 \mod 4 = 3 \) perchè: \( 15/4 = 3 \text{(quoziente)} + 3 \text{(resto)} \). In questo caso l’operazione assicura che il numero casuale sia uniformemente distribuito: ogni numero ha la stessa probabilità di uscire da queste operazioni (non deterministico). Abbiamo ora due valori completamente casuali.

Studiamo la parte RNG (generatore casuale di numeri). L’articolo fa riferimento a un LCG (generatore congruenziale lineare) che è uno dei più semplici ma efficienti generatori odierni, fa parte del campo dei generatori deterministici ma grazie al passaggio precedente diventa imprevedibile. É di forma:

\(Y = aX\text{(seed)} + c \text{(numero tentativi)} \mod m \).

Precisamente la parte casuale è il seed (seme), chiamato così perchè è il punto di partenza della generazione. Periodicamente aggiorniamo il seed con i valori casuali generati con i processi precedentemente illustrati per mantenere un’entropia alta nel sistema. A questo punto l’articolo non ci informa per cosa sia usata la N (numero tentativi per riordinare la lista) ma possiamo ipotizzare che sia usato nel generatore come incremento in quanto “a” e “m” sono dei valori troppo sensibili e su cui vogliamo avere controllo. Non entrerò nel dettaglio degli LCG poichè lontano dallo scopo dell’articolo. Di seguito porterò dei grafici della generazione.

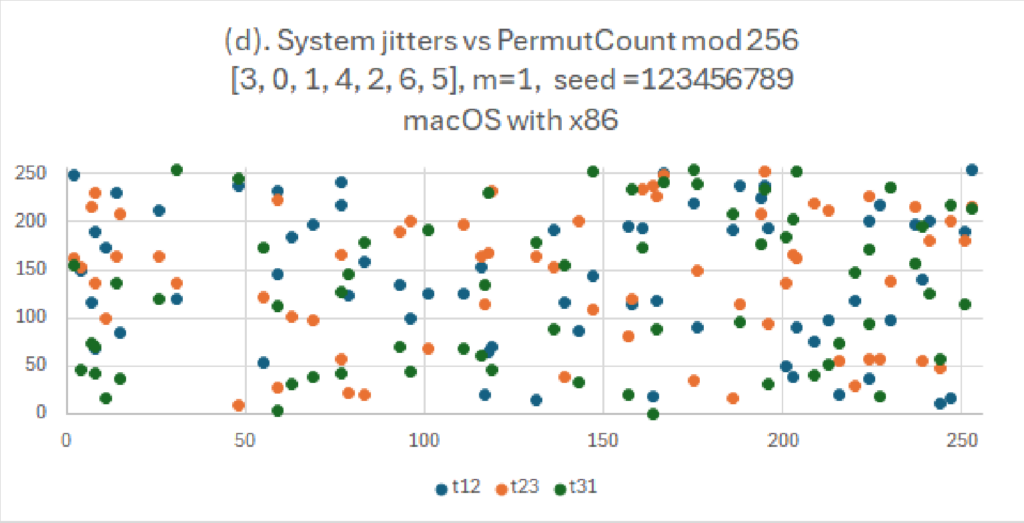
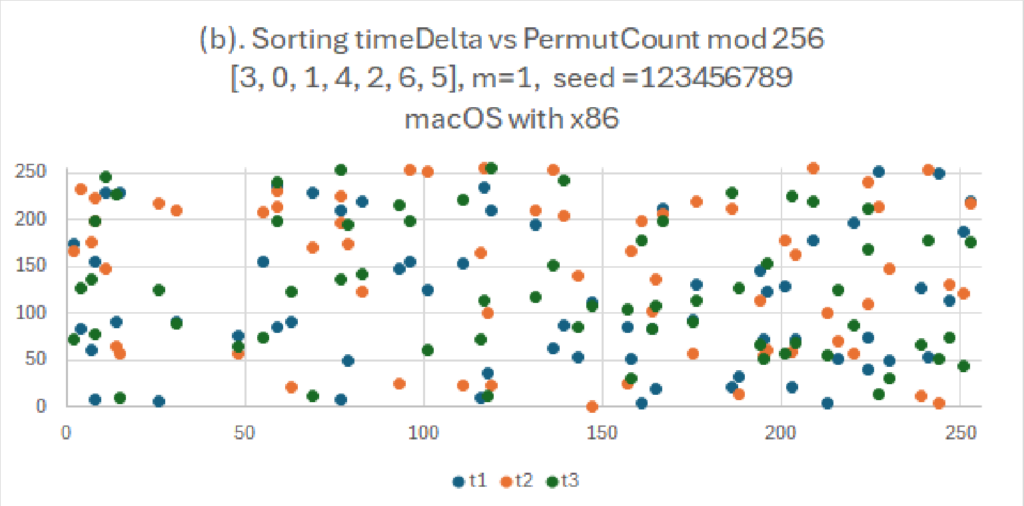
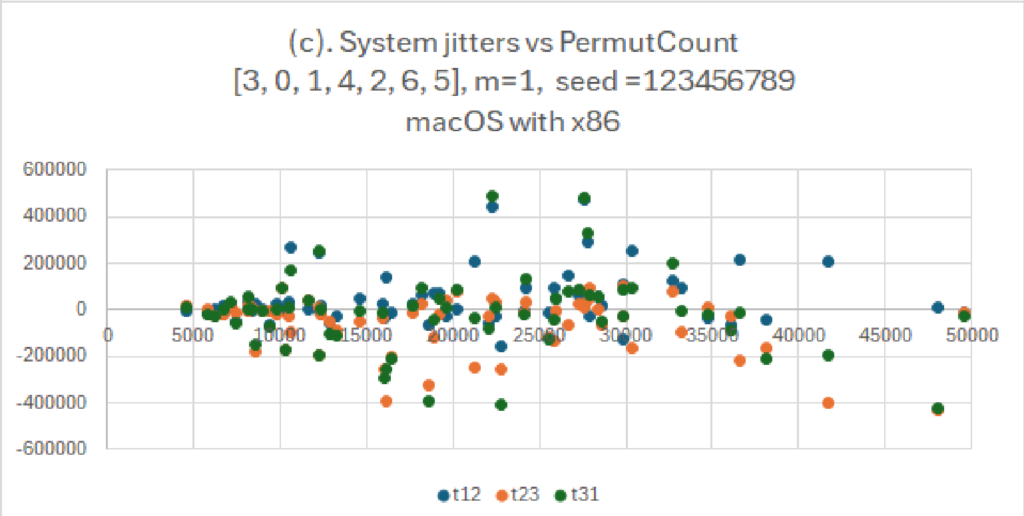
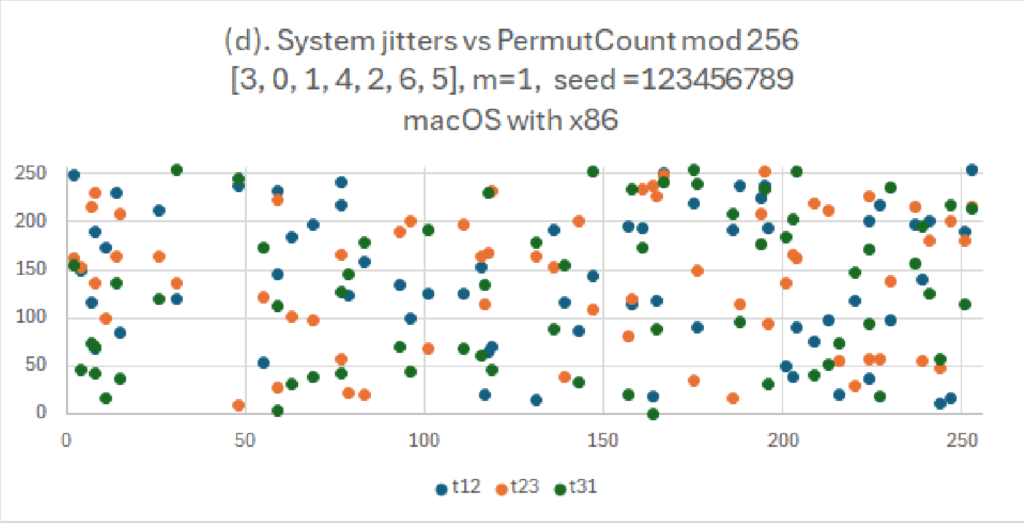
I grafici sembrano complessi ma sono di facile lettura. Mostrano la dispersione di numeri per due diversi tipi di generatori casuali. Come titolo abbiamo le caratteristiche del generatore e l’algoritmo usato. Qui si evince come l’algoritmo illustrato: “(d) System jitters vs PermutCount mod 256” abbia una distribuzione veramente casuale quindi i punti colorati sono molto lontani fra di loro.

Notiamo anche che grazie alle tecniche usate, nonostante i nostri dati di partenza siano gli stessi (seme, lista da riordinare, permutazione), l’algoritmo genera valori completamente diversi.

I risultati di questo algoritmo sono significativi, il primo passo verso la nuova sicurezza informatica. Il linguaggio di prova è stato Java con implementazioni sulle principali piattaforme e hardware usate: Windows, MacOs (x86), MacOs(ARM).

Gli studi sulla generazione di numeri casuali sono sull’entropia dei bit generati e la distribuzione. Il calcolo sull’entropia di shannon del sistema su 8 bit è di 7.99981 bit di casualità con un minimo prodotto dal secondo test “Chi-square” di 262 (vicino al nostro ideale di 256), i grafici dimostrano sulla generazione di 1.000.000 di numeri che la generazione è uniforme e robusta. Non ci sono dati sui tempi di esecuzione, sappiamo solo che Windows ha tempi di esecuzione più lenti mettendoci circa tre volte e mezzo il tempo di esecuzione rispetto ai dispositivi Mac. La soluzione è portabile e software quindi può essere usata su diversi computer senza problemi o necessità di modifiche nel codice.

I passi per il futuro sono tanti, abbiamo una base notevole e possiamo usarla per diversi scopi. Il primo passo è l’implementazione di questa generazione di algoritmi all’interno di programmi crittografici. L’obiettivo diventa poi di ottimizzare il processo di generazione per generazione ad alta frequenza di numeri casuali per diversi scopi quali: servizi web, simulazioni di processi fisici ed estrazioni di dati casuali.